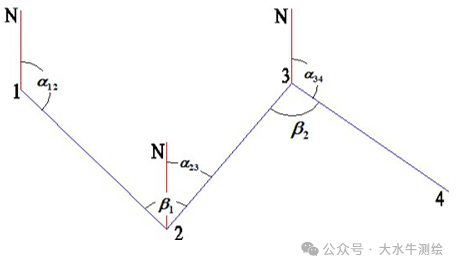
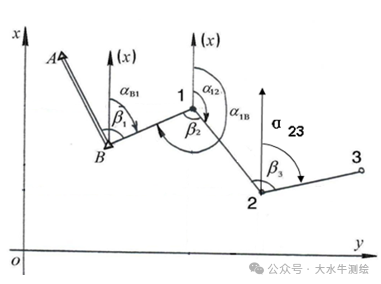
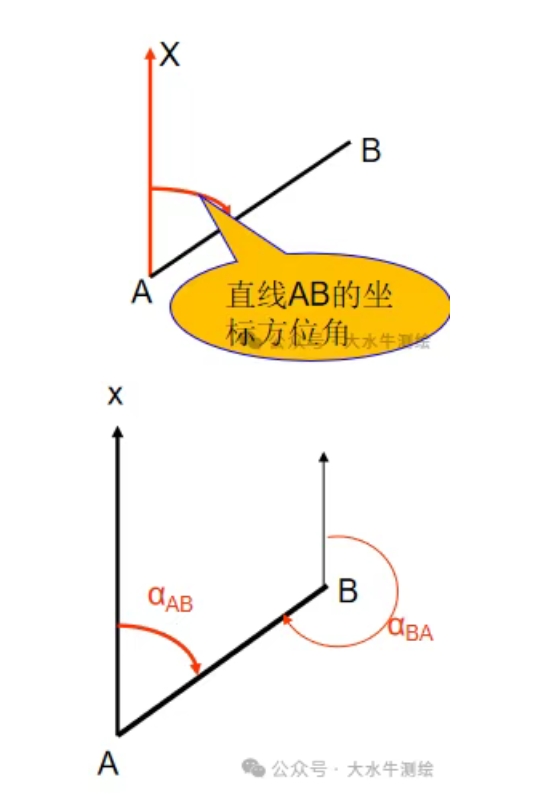
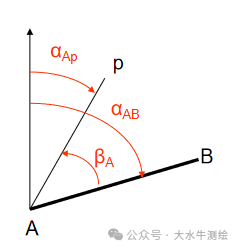
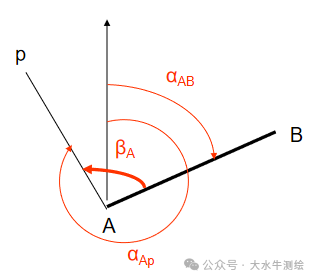
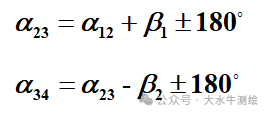在工程测量领域,全站仪导线测量是获取平面控制点坐标的核心手段之一,而坐标方位角的推算则是这一过程中连接已知数据与未知控制点的关键环节。 平面控制点坐标计算的基本内容有:坐标方位角的推算、坐标反算和坐标正算。本期我们先来简单看一下坐标方位角的推算。 一、坐标方位角的推算 坐标方位角:从平行于坐标轴纵轴的北端顺时针旋转至某直线的水平角为该直线的坐标方位角,方位角的角值范围在0°~360°之间。 正反坐标方位角: 根据一条已知边方位角和观测的已知边与未知边之间的水平角,来推算未知边方位角称为坐标方位角的推算。坐标方位角的推算示例一已知边AB的方位角为αAB;为求观测边Ap的方位角αAp,在A点测量出AB与Ap的水平夹角β。根据方位角的定义(从轴北方向开始,顺量),结合图3容易得到:αAp=αAB+βA。 注意:两条直线的起点须相同! 利用αAP=αAB+βA推算方位角需注意,βA是“左角”,即站在起点(角顶A)、面向终点(前进方向的未知点p)时,位于观测者左手边的角度。左角也可理解为“从已知边顺转至未知边的水平角”。如果观测的水平角不是左角而是“右角”(即位于前进方向右边的角度,或从已知边逆转至未知边的水平角),如下中图中的βA,则应按下式推算未知边的方位角:αAp=αAB-βA。 同样应注意:两条直线的起点须相同!计算结果小于0°时需加360°,如下图。 坐标方位角的推算示例二根据已知边1-2的方位角和观测的水平角β,推算2-3边的方位角,可以分成两步进行计算: 1)根据1-2的方位角求2-1的方位角:α21= α12±180°; 2)根据2-1边的方位角和观测的水平角β ,求2-3边的方位角:α23= α21+β,若观测的β为右角时:α23= α21-β; 合起来就有:α23= α21±β=α12±β±180°。 综上所述方位角推算的公式为: 如下图所示则有: 例如:在下图中,A、B为已知点,1、2、3为待测的未知点。已知αAB=152° 32′50 ”,各转折角分别为:92° 25′58 ” ,107° 50′30 ”,126° 43′12 ”,试推算2-3的方位角。 解: β1为左角, ∴αB1=αAB+β1 ±180° =152° 32′50"+92° 25′58" ±180° =244° 58′48" ±180° =64° 58′48" β2为右角, ∴α12=αB1-β2 ±180° =-42° 51′42" ±180° =137°08′18 " β3为左角, ∴ α23=α12+β3 ±180°= 83°51′30 "
![]()
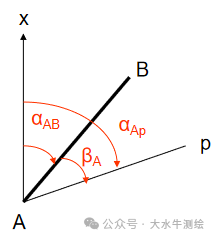
计算结果大于360°时须减去360°,如下图4。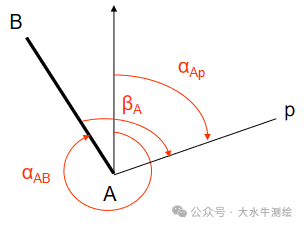
![]()